R là tập hợp số gì? Ví dụ về tập hợp số R
R là tập hợp số gì? Ví dụ tập hợp R
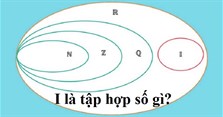
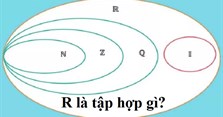
R là tập hợp số thực, bao gồm tất cả các số hữu tỉ và số vô tỉ. Đây là tập hợp số lớn nhất. Tất cả các tập hợp số còn lại đều là tập con của nó.
Ví dụ về số thực R:
3, 
, -0,245, , đều là số thực.
R+ là tập hợp số gì?
R+ là tập hợp số thực dương. Ví dụ: 1, , .
R* là tập hợp số gì?
R* là tập hợp số thực khác 0.
Tập hợp R có số 0 không?
Tập hợp R có bao gồm số 0. Số 0 trong tập hợp R không phải là số thực dương, cũng không phải số thực âm.
Biểu diễn trục số R
Mỗi số thực được biểu diễn bởi một điểm trên trục số. Nói cách khác, mỗi điểm trên trục số điều biểu diễn một số thực.
Chỉ có tập hợp số thực mới lấp đầy được trục số.
Tính chất và các phép tính của tập hợp R
Với a, b, c là số thực:
1). Số đối của số thực a là -a. Số đối của số 0 là 0.
2). Số thực lớn hơn 0 là số thực dương. Số thực nhỏ hơn 0 là số thực âm. Số 0 không phải là số thực âm, cũng không phải là số thực dương.
3). Nếu a<b và b<c thì a<c.
4). Tính chất của phép cộng các số thực:
Giao hoán: a + b = b + a
Kết hợp: (a + b) + c = a + (b + c)
Cộng với số 0: a + 0 = 0 + a = a
Cộng với số đối: a + (-a) = (-a) + a = 0
5). Tính chất của phép nhân các số thực:
Giao hoán: a.b = b.a
Kết hợp: (a.b).c = a.(b.c)
Bất kỳ số thực nào nhân số với 1 cũng bằng chính nó: a.1 = 1.a = a
Phân phối đối với phép cộng: a.(b + c) = a.b + a.c
Với mỗi số thực a ≠ 0, số nghịch đảo của a là sao cho a. = 1
6). Phép tính lũy thừa với số mũ tự nhiên của số thực:
