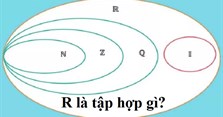
Q là tập hợp số gì? Ví dụ về tập hợp số Q dễ hiểu

Cập nhật: 07/10/2024

Q là tập hợp số gì? Ví dụ

Q là tập hợp số hữu tỉ (gồm những số có thể biểu diễn dưới dạng phân số $\frac{a}{b}$ với a, b ∈ Z và b $\ne$ 0).

Ví dụ số hữu tỉ:

Các số -5; $2\frac{5}{9}$ ; -0,52 đều là số hữu tỷ vì chúng có thể viết dưới dạng phân số với tử số và mẫu số đều thuộc tập hợp Z:

$-5=\frac{-5}{1}$ ; $2\frac{5}{9}=\frac{23}{9}$ ; $0,52=\frac{52}{100}$

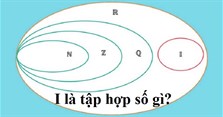
Q* là tập hợp số gì?

Q* là tập hợp số hữu tỉ khác không. Như vậy, Q* là tập hợp con của Q.

Tập hợp số Q có bao gồm số 0?

Số 0 là một phần tử của tập hợp số Q, bởi vì nó có thể biểu diễn dưới dạng phân số với tử số bằng 0 và mẫu số là một số nguyên khác 0 bất kỳ: $0=\frac{0}{1}=\frac{0}{234}=\frac{0}{-2}$

Biểu diễn tập số Q trên trục số

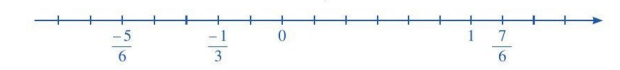
Tính chất của tập số Q

1). Tính so sánh

Trên trục số, hai số hữu tỉ phân biệt có điểm biểu diễn nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0 được gọi là hai số đối nhau. Số đối của số hữu tỉ a, ký hiệu là -a. Số đối của 0 là 0.
Trong hai số hữu tỉ khác nhau thì luôn có một số nhỏ hơn số kia. Ví dụ với a và b là hai số hữu tỉ, trong đó a nhỏ hơn b thì ta có thể viết a < b hoặc b > a.
Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương, số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.
Số hữu tỉ 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.
Với a, b, c là số hữu tỉ, nếu a < b và b < c thì ta có a < c.

2). Tính chất của phép cộng các số hữu tỉ

Phép cộng các số hữu tỉ có các tính chất: giao hoán, kết hợp, cộng với số 0, cộng với số đối.
Ta có thể chuyển phép trừ cho một số hữu tỉ thành phép cộng với số đối của số hữu tỉ đó.

Ví dụ: $\frac{1}{2}-\frac{1}{4}=\frac{1}{2}+\left(\frac{-1}{4}\right)$

3). Tính chất của phép nhân các số hữu tỉ

Phép nhân các số hữu tỉ có các tính chất: giao hoán, kết hợp, nhân với số 1, phân phối.

4). Phép lũy thừa của một số hữu tỉ với số mũ tự nhiên

Với x ∈ Q và m; n ∈ tập hợp số N ta có:

Lũy thừa bậc n của một số hữu tỉ x ký hiệu là x^n, là tích của n số hữu tỉ x. Trong đó x là cơ số, n là số mũ. Quy ước: x¹ = x.
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: x^m.xⁿ = x^m+n
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: x^m:xⁿ = x^m-n(với $x\ne0$ , $m\ge n$ ).
Quy ước: x⁰ = 1 ( $x\ne0$ ).